【数的推理で7割とる】誰でもできる勉強方法と解き方のコツを解説！

数的推理は公務員試験における重要科目であり、苦手意識を持っている方も多いはず。

そこで本日は、

こういった悩みを解決できる記事を用意しました。

この記事で紹介する「数的処理の勉強方法や解き方のコツ」を実践すれば、数的推理で7割は安定して得点できるようになります！

なぜなら、僕もこの方法を用いて勉強するようになってから安定して数的推理の点数を取れるようになったからです。

それまでの、僕は4〜5割取れれば良い方。高校時代もがっつり文系で数学は大の苦手科目でした、、、

そんな僕でも、7割は安定して取れる！と自信を持って言えるようになったので、ぜひこの記事を読み込んで、数的推理を得点源にしちゃってください！

初めに僕が使っていた参考書をご紹介しておきます。この参考書で本番の数的推理は7割取れました！かなり良書だと思うので、参考書で迷っている方はぜひ！

↑この2冊は解説がめちゃくちゃわかりやすいので数学系が苦手な方はかなりオススメです！

そもそも【数的推理】って？？

まずは、前提を押さえておきましょう。

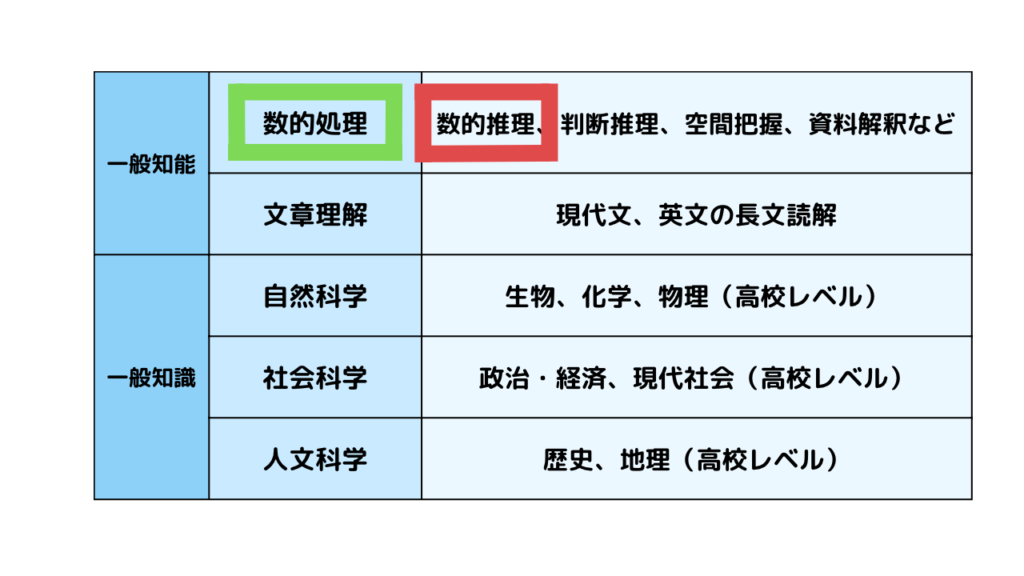
数的処理には4つの単元がありその科目の中の1つというわけですね。

数的推理と聞いて「なにそれ？？」と感じた方も多いと思います。

それもそのはず、数的推理という科目は、公務員試験独自の科目となっていて、与えられた情報から解決策を見つける能力を見極めるための問題となっています！

主な出題内容

数的推理の主な出題内容は

数の性質	・倍数・約数 ・素数・素因数分解 ・余剰 ・数列 ・N進法 ・魔法陣
場合の数・確率	・場合の数 ・順列 ・確率
文章題	・方程式 ・割合・比 ・速さ 　旅人算・流水算・通過算・時計算など ・仕事算 ・平均
図形	・多角形 ・円 ・相似・合同 ・立体図形

主にこのような内容となっています。

安心してください。これから紹介する勉強方法や解き方のコツを学べば、どんなに数学が苦手な方でも7割は安定して取れるようになります！

諦めず、一緒に頑張っていきましょう！

数的推理が重要科目と言われる理由【めちゃくちゃ大切です！】

公務員試験について調べていくと必ず「数的推理は最重要科目」とか「まず勉強を始めるなら数的推理から」という言葉に出合うと思います。

その理由はシンプルで「出題数が多いから」です。

職種	過去の出題数（数的推理のみ抜粋）
国家一般職	5問
国家専門職	5問
裁判所一般職	6問
東京都Ⅰ類B	6問
特別区Ⅰ類	5問
地方上級全国型	5問
市役所A日程	6問

40点満点中6割以上（24点以上）を取れば合格ラインにのると言われている公務員試験において、数的推理だけで約6点（合格点のうち4割！！）を占めるんです。

ここを対策せずに、みすみす落とすのはかなり勿体無い！というか、多分受からない！

だからこそ、「数的推理は大切！」とか「最初に勉強すべき！」と言われているんです。

【点数が伸びる！】勉強する際の4つのポイント！

ここからは、点数を伸ばすための効果的な勉強方法を紹介していきます。

「勉強しているけど点数が伸びない」という方は少なくないと思います。当時の僕もそうでした。

がむしゃらに問題集を解いて勉強していた気になっていましたが、模試で全滅、、、

何か変えないといけないと思い、参考書やYouTubeなどで情報を集めて実践しました。

その結果、自分の中で効果のある勉強方法がわかってきました。それが以下の4つです。

それぞれ解説していきます！

①出題パターンを確認する

問題を解く際に、まずは問題を読みますよね。

その時に、すぐに解法を思い浮かべるのではなく、まずは下記表のどの出題パターンに当てはまるのかを確認することが大切です。

数の性質	・倍数・約数 ・素数・素因数分解 ・余剰 ・数列 ・N進法 ・魔法陣
場合の数・確率	・場合の数 ・順列 ・確率
文章題	・方程式 ・割合・比 ・速さ 　旅人算・流水算・通過算・時計算など ・仕事算 ・平均
図形	・多角形 ・円 ・相似・合同 ・立体図形

なぜ、出題パターンの確認が大切かというと

出題パターンには典型的な解法が存在するから

ジャンルを問わない莫大な量の解法を覚えるよりも、出題パターンの解法を覚えた方がはるかに効率が良いですし、解く時間も早くなります。

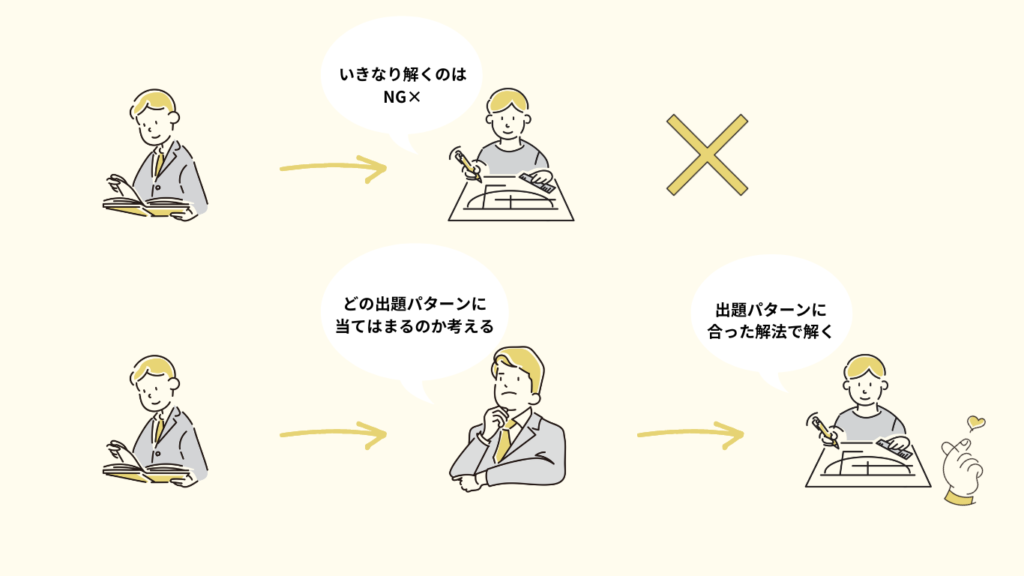
さらに、問題集は出題パターンごとに問題が固まっているため、出題パターンを日頃の勉強で意識しないことが多いんです。

本番は、どの順番でどのような問題が出るかわかりませんからね。

まずは出題パターンの確認！ここを意識してみてください！

②出題パターンの典型的な解法を暗記する

2つ目が、出題パターンの典型的な解法の暗記です。

画像の通り、数的推理には出題パターンごとに典型的な解法が存在します。まずは、その解法を覚えること！

この2つを意識するだけ！
ここの意識の差で点数が伸びるか伸びないかが決まってきます！

よくありがちなのが「あれもこれもと暗記の範囲を広げすぎてしまうこと」

公務員試験は過去に出題された類似問題が多く出題されます。そのため、頻出問題に絞って深く学習した方が圧倒的に効率が良く点数が伸びます！

「問題文のキーワードと解法を結びつける」については、次の章で実際の問題を使って解説します！

③時間を測りながら解く

3つ目は、時間を測りながら解くです。

公務員試験は全40問〜50問出題され、その問題数を「2時間30分」で解く必要があります。

単純計算、1問にかけられる時間は3分ほど！

この短い時間の間に

• 問題の読解
• 出題パターンの確認
• 解法の把握
• 解く手順

などを考えて答えを導き出すわけです。

さらに、本番は独特な雰囲気と緊張感で時間感覚が麻痺します。日頃から時間感覚を意識して解いておくことが大切です。

④問題演習を繰り返す【3周は必須】

4つ目が、問題演習を繰り返すです。

あとは、①〜③を意識しながら、ひたすら問題演習を繰り返すだけ！

僕個人の意見ですが、最低でも3周は同じ問題集を解く必要があると考えています。

1周目	わからないながらも、問題 → 出題パターンの確認 → 解法 を意識して解く
2周目	解法が浮かぶ問題には⚪︎、解法が浮かばない問題には×をつけて理解度を把握する
3周目	解法が浮かばない問題を中心に解法の暗記漏れを埋める

解法が浮かぶ問題に関しては、もう一度解く必要はなく「問題をみる → 正解までの手順を頭の中で思い浮かべる」これだけでOKです。

必要に応じて4周、5周と回数を増やしていきながら対応していきましょう。

数的推理を解くコツ【流れを細かく分解して解説！】

ここからは、数的推理の問題を解く際の考え方を実際の問題を使って、流れで説明していきます。

数的推理の問題を解く時の頭の中はこんなイメージ！

安心してください！1つずつ実際の問題を例に解説していきます！

①求められているもの（ゴール）を確認

ここで重要なのが、問題文にあるキーワード！

ここでは「時間」「距離」が問題文に出てきているのでこの問題は「速さ」かな？と仮説を立てておきます！

どの問題にも、出題内容に関連したキーワードが出てきます。そのキーワードと解法パターンを結びつけておくと、かなりスムーズに答えられるようになってきます。

②出題パターンを把握

先ほどの問題文のキーワードをもとに、どの出題パターンに当てはまるか検討します。

「時間」「距離」 → 速さの問題かとなるわけです！

そして速さの公式である、速さ×時間=距離が頭に入っていれば、この問題の出題パターンが「速さ」だと気づくはずです！

③現在ある確実な情報を確認

ここでやっと問題に入って行きます。（慣れてくれば①②は無意識でできるようになります。）

まずは、問題文の中にある確実な情報を確認します。

今回わかっているのが、以下の3つです。

ここから、Aがゴールした時間を求める解法の手順を考えていきます！

④出題パターンの解法を思い描く

AとBがゴールする時間の比が9：10なので、その差の【1】がゴールの差【4分】になるわけです。

Aがゴールした時、Bは720m後ろにいたため、Aは計7200m走ったことになります。

よって、7200m➗200m/分＝36分

正解は、【5】の36分になります。

このように①〜④を意識して繰り返し問題演習を行い、解法を暗記することで7割は誰でも目指せます！

まとめ【数的推理は得点源になる！】

本日は、数的推理の勉強方法と解き方のコツを解説しました！

数的推理は、かなり数学的な問題に近いため苦手意識を持つ方もいると思います。

しかし、出題パターンの解法を暗記し、問題演習を繰り返し行うことで7割は安定して得点することができます！

数的推理を得点源にして、公務員試験を有意に進めましょう！

この記事が、みなさんの参考になれば嬉しいです！